实体对齐文献阅读笔记¶
阅读实体对齐相关文献的笔记
1. Translating Embeddings for Modeling Multi-relational Data¶
如果一个三元组成立,则应该满足$\mathbf{h}+\mathbf{l}\approx\mathbf t$

即$d(\mathbf h+\mathbf l,\mathbf t)$ 尽可能小,而$d(\mathbf h'+\mathbf l,\mathbf{t'})$尽可能大
其中$\mathbf{h'\ t'}$表示不可能对齐的实体对,通过替换种子实体中头或尾实体为随机实体得到
所以就得到了上面的损失函数,$[x]_+$表示若$x>0$则取$x$,若$x<0$则取$0$,由此得到,如果$\gamma$较大则训练时间较长,因为需要较多时间让$\mathbf L$到达$0$,否则需要时间较短
最后使用随机梯度优化进行训练

2. A Joint Embedding Method for Entity Alignment of Knowledge Bases¶
在TransE的基础上,修改了损失函数
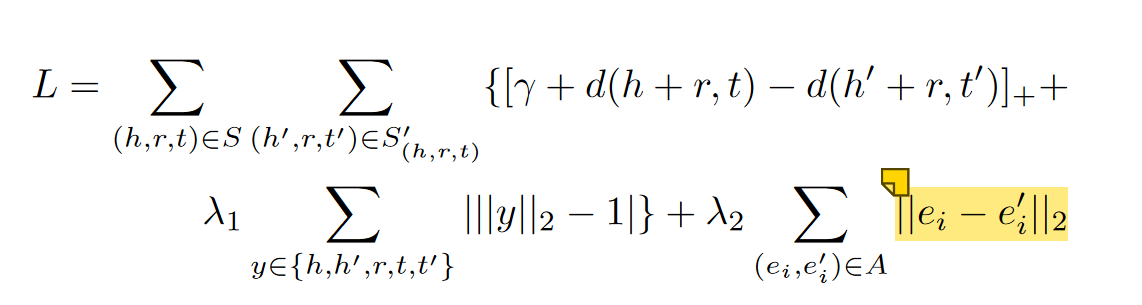
其中二范数接近于1可以避免通过最小化嵌入来最小化损失函数,这样就不是由于对齐而是由于嵌入的减小才导致的损失函数减小
矩阵M如下计算

3. Multilingual Knowledge Graph Embeddings for Cross-lingual Knowledge Alignment¶
采用传统TransE,但是损失函数重新定义$S_K=\sum\limits_{L\in\{L_i,L_j\}}\sum\limits_{(h,r,t)\in G_L}||\mathbf{h+r-t}||$
即直接利用所有三元组衡量嵌入的效果
- 这样做可以让单语种保留原有特性,因为单个语种的三元组只在自己内部训练
- 不同语言可以并行训练
对齐模块的损失函数
$S_A=\sum\limits_{T,T'\in\delta(L_i,L_j)}S_a(T,T')$
其中$S_a(T,T')$穷举所有种子三元组对
其中$S_a$包含5种变体
- 基于距离的坐标轴转换:$S_{a_1}=\mathbf{||h-h'||+||t-t'||}$,$S_{a_2}=\mathbf{||h-h'||+||r-r'||+||t-t'||}$即转换一方的坐标轴使两个对齐
- 转换向量:$S_{a_3}=\mathbf{||h+v^e_{ij}-h'||+||r+v^r_{ij}-r'||+||t+v^e_{ij}-r'||}$
- 线性转换:$S_{a_4}=\mathbf{||M^e_{ij}h-h'||+||M^e_{ij}t-t'||}$,$S_{a_5}=\mathbf{||M^e_{ij}h-h'||+||M^r_{ij}r-r'||+||M^e_{ij}t-t'||}$
其中$S_{a_3}-S_{a_5}$可逆,这也就对应模型的5种变体
整体损失函数$J=S_K+\alpha S_A$
利用随机梯度下降优化,在每一个epoch中,分别在不同的组优化$\theta\leftarrow\theta-\lambda\nabla_\theta S_K$和$\theta\leftarrow\theta-\lambda\nabla_\theta\alpha S_A$
依然应用二范数趋近于1来防止训练过程中通过缩小嵌入向量的方式来最小化损失函数
项目地址:https://github.com/muhaochen/MTransE
4. Cross-lingual Entity Alignment via Joint Attribute-Preserving Embedding¶
结构嵌入(TransE)只约束学习到的表示在每一个关系三元组内部兼容,导致由于关系三元组的稀疏(某些实体只分布在一个关系三元组中),某些实体的分布是无序的。为了缓解这个问题,本文引入属性三元组帮助实体嵌入,因为可能对齐的实体常常有高度相似的属性值。使用属性值和范围类型,忽略具体的属性值。通过属性嵌入获取跨语种和单语种属性的关系,并计算基于属性嵌入的实体相似度,结合结构嵌入,通过聚类有高度属性联系的实体增强表示。
对于三元组$tr=(h,r,t),f(tr)=||\mathbf{h+r-t}||^2_2,tr'$为破坏后的三元组,即替换头或尾实体为随机实体。
结构嵌入损失函数(TransE):最小化$O_{SE}=\sum\limits_{tr\in T}\sum\limits_{tr'\in T'_{tr}}(f(tr)-\alpha f(tr')),\alpha\in[0,1]$
种子实体共享相同嵌入,作为训练时链接两个KB的桥。具有相同头尾实体的可能是同一关系;具有相同头和关系的可能是同一尾
属性嵌入目标函数:最小化$O_{AE}=-\sum\limits_{(a,c)\in H}\omega_{a,c}\cdot logp(c|a)$,其中$logp(c|a)=log\sigma \mathbf{(a\cdot c)}+\sum\limits_{a,c'\in H'_a}log\sigma(-\mathbf{a\cdot c}),\sigma(x)=\frac{1}{1+e^{-x}}$
属性嵌入利用了skip-gram模型,利用属性预测相关属性。属性相关指两个属性在同一实体、对应种子实体。如果有相同类型,则相关性更强($\omega=1,2$)。$H_a'$是根据负对数基生成的错误对,假设都是错误的
实体相似度计算:实体利用正规化的属性嵌入表示$\mathbf e=[\sum\limits_{a\in A_e}\mathbf a]_1$
利用余弦距离表示实体相似度$sim(\mathbf{e,e'})=\mathbf{e\cdot e'}$,可以利用实体嵌入向量组成矩阵计算相似度矩阵$S^{i,j}=E_{AE}^{(i)}E_{AE}^{(j)T}$
利用相似度的平均值$\tau$,$S_{i,j}>\tau\rightarrow S_{i,j}=1,else\ S_{i,j}=0$
联合嵌入目标函数$O_{joint}=O_{SE}+\delta O_{S}$
其中$O_{S}=||E_{SE}^{(1)}-S^{(1,2)}E^{(2)}_{SE}||^2_F+\beta(||E_{SE}^{(1)}-S^{(1)}E^{(1)}_{SE}||^2_F+||E_{SE}^{(2)}-S^{(2)}E^{(2)}_{SE}||^2_F)$
训练时利用AdaGrad优化,并且可以分别优化$O_{SE}$和$\delta O_S$
训练结束后计算$\mathbf D=\mathbf E^{(1)}_{SE}\mathbf E^{(2)T}_{SE}$,将相似度降序排列,前几个作为对齐结果
项目地址:https://github.com/nju-websoft/JAPE
5. Iterative Entity Alignment via Joint Knowledge Embeddings¶
使用经典TransE: $K_T=\sum\limits_{T\in \{T_1,T_2\}}\sum\limits_{(h,r,t)\in T}L(h,r,t)$
$L(h,r,t)=\sum\limits_{(h',r',t')\in T^-}[\gamma+E(h,r,t)-E(h',r',t')]_+$
同时采用PTransE的策略,定义关系路径集$P(h,t)=\{p|\forall e\in E,r_1,r_2\in R,(h,r_1,e),(e,r_2,t)\in T,p=r_1\circ r_2\}$,如果一个关系路径和关系作用相同,$p\in P(h,t),(h,r,t)\in T$,定义路径嵌入$\mathbf{p\simeq r}$,$E(p,r)=||\mathbf{p-r}||=||\mathbf{p-(t-h)}||=E(h,p,t)$
评分函数$K_P=K_T+\sum\limits_{T\in \{T_1,T_2\}}\sum\limits_{(h,r,t)\in T}[\frac 1 Z\sum\limits_{p\in P(h,t)}R(p|h,t)L(p,r)],Z=\sum\limits_{p\in P(h,t)}R(p|h,t),R(p|h,t)$指在给定$(h,t)$时$p$的可靠性
$L(p,r)=\sum\limits_{(h,r',t)\in T^-}[\gamma+E(p,r)-E(p,r')]_+$
Modeling Relation Paths for Representation Learning of Knowledge Bases
利用路径资源约束算法表示路径的可靠性:h中有一定资源,通过p流向t,通过测量流向t的资源量反映p的可靠性
对于路径$S_0\rightarrow^{r_1}S_1\rightarrow^{r_2}\rightarrow^{r_3}...\rightarrow^{r_l}S_l$,$\forall\ entity\ m\in S_i,S_{i-1}(\cdot,m)$是
$m$通过$r_i$的直接前置,$S_{i}(n,\cdot)$是$S_{i-1}$中任意$n$通过$r_i$的直接后置,$R_p(n)$是从实体$n$获取到的资源
定义流向$m$的资源为$R_p(m)=\sum\limits_{n\in S_{i-1}(\cdot,m)}\frac{1}{|S_i(n,\cdot)|}R_p(n)$
$R_p(h)=1,R_p(h,t)=R_p(t)$
联合嵌入采用类似MTransE中的$S_{a_3},S_{a_4}$,即
- 转换模型:$E(e_1,e_2)=||\mathbf{e}_1+\mathbf{r}^{(E_1\rightarrow E_2)}-\mathbf{e}_2||$
- 线性变换模型:$E(e_1,e_2)=||\mathbf{M}^{(E_1\rightarrow E_2)}\mathbf{e}_1-\mathbf{e}_2||$,$\mathbb{L}$作为种子
- 前两种方法的分数函数为$J_{T/L}=\sum\limits_{(e_1,e_2)\in \mathbb{L}}\alpha E(e_1,e_2)$
- 参数共享模型:$e_1\equiv e_2,(e_1,e_2)\in\mathbb{L},J_P=0$
迭代训练:让新对齐的实体作为新种子添加,分为硬对齐($\mathbf e_1,\mathbf e_2\leftarrow\frac 1 2(\mathbf{e}_1+\mathbf{e}_2)$)和软对齐(减少误差传播的影响):
赋予每一对齐的实体一个可靠性得分$R(e_1,e_2)=sigmod(k(\theta-E(e_1,e_2)))$
$\mathbb{M}$是不断添加新种子的集合
则得分函数$I_S=\sum\limits_{(e_1,e_2)\in\mathbb{M}}R(e_1,e_2)(H_{(e_1,e_2)}+H_{(e_2,e_1)})$
$H_{(e_1,e_2)}=\sum\limits_{(e_1,r,t)}U(e_2,r,t)+\sum\limits_{(h,r,e_1)}U(h,r,e_2)$
TransE中$U(h,r,t)=L(h,r,t)$,PTransE中$U(h,r,t)=L(h,r,t)+\frac 1 Z\sum\limits_{p\in P(h,t)}R(p|h,t)L(p,r)$
使用随机梯度下降训练,在软对齐中限制新增种子数量
6. Bootstrapping Entity Alignment with Knowledge Graph Embedding¶
$x,y$是待对齐的实体,对于$\tau=(h,r,t),f(\tau)=||\mathbf{h+r-t}||$
损失函数:$O_e=\sum\limits_{\tau\in T^+}[f(\tau)-\gamma_1]_++\mu\sum\limits_{\tau'\in T^-}[\gamma_2-f(\tau')]_+$。绝对小的嵌入可以防止空间中嵌入漂移的问题
由于$f(\tau')- f(\tau)\gt\gamma_2-\gamma_1$,所以也是一个margin-based,即可以控制$\gamma_1$和$\gamma_2$的值确定训练结果
Learning knowledge embeddings by combining limit-based scoring loss
负采样策略:如果随机替换则对于一些本来就相差很远的三元组来说,对于整体训练时没有帮助的。所以替换相近的三元组。
给定一个要替换的$x$,在嵌入空间中选择最相似的$s=\lceil(1-\epsilon)N\rceil,\epsilon\in[0,1)$个候选,利用余弦距离确定和$x$的相似度
在三元组中交换对齐的实体,来校准两个KG中的实体嵌入
$T^s_{(x,y)}=\{(y,r,t)|(x,r,t)\in T_1^+\}\cup\{(h,r,y)|(h,r,x)\in T_1^+\}\cup\{(x,r,t)|(y,r,t)\in T_2^+\}\cup\{(h,r,x)|(h,r,y)\in T_2^+\}$
这样就可以得到一个完整的$T^+=T_1^+\cup T_2^+\cup T^s$,然后负采样得到$T^-$
采用了Bootstraping策略,并且有编辑策略
在第$t$轮迭代解决如下优化问题,$max\sum\limits_{x\in X'}\sum\limits_{y\in Y'_x}\pi(y|x;\Theta^{(t)})\cdot\psi^{(t)}(x,y),\pi(y|x;\Theta)=\sigma(sim(\mathbf{x,y})),\Theta$是嵌入,$\sum\limits_{x'\in X'}\psi^{(t)}(x',y)\le1,\sum\limits_{y'\in Y'_x}\psi^{(t)}(x,y')\le 1,Y'_x=\{y|y\in Y'\ and\ \pi(y|x;\Theta^{(t)})\gt\gamma_3\},\gamma_3$是判定两个实体是否对齐的阈值
如果在$t$轮$x$标签是$y$则$\psi^{(t)}(x,y)=1$,否则为$0$。这是指标函数。在第$t$轮使用新对齐的实体对引导下一步对齐
为了提升对齐准确率,减少错误率,基于一对一对齐约束,提出错误修复方法
$\Delta^{(t)}_{(x,y,y')}=\pi(y|x;\Theta^{(t)})-\pi(y'|x;\Theta^{(t)})$
如果$\Delta>0$则说明有$y$比$y'$更适合和$x$对齐
$\phi_x$用于描述$x$的概率分布,即x获得所有标记的可能性
$\phi_x(\hat y)=\begin{cases}\mathbf 1,x\ is\ labeled\ as\ \hat y\\\frac 1 {|Y'|},x\ is\ unlabeled\end{cases}$
嵌入的目标函数$O_a=-\sum\limits_{x\in X}\sum\limits_{y\in Y}\phi_x(y)log\pi(y|x;\Theta)$
全局目标函数$O=O_e+\mu_2\cdot O_a$
利用AdaGrad随机梯度下降优化,嵌入的二范数约束为1
项目地址:https://github.com/nju-websoft/BootEA
7. Co-training Embeddings of Knowledge Graphs and Entity Descriptions for Cross-lingual Entity Alignment¶
同时采用了实体嵌入和实体描述来对齐实体,先使用实体嵌入找到对齐的实体,再使用实体描述找到另一部分对齐的实体

ILL:语言间链接
实体嵌入模型采用经典TransE,$S_k=\sum\limits_{L\in\{L_i,L_j\}}\sum\limits_{(h,r,t)\in G_L\wedge(\hat h,r,\hat t)\notin G_L}[f_r(h,t)-f_r(\hat h,\hat t)+\gamma]_+$
实体对齐模型采用线性转换$S_A=\sum\limits_{(e,e')\in I(L_i,L_j)}||\mathbf M_{ij}\mathbf e-\mathbf e'||_2$
实体描述采用注意力门控循环单元
$A(a_{ij})\odot B(b_{ij})=C(c_{ij})$是Hadamard product,$c_{ij}=a_{ij}\times b_{ij}$
《Deep Learning: Adaptive Computation and Machine Learning series》
https://zhuanlan.zhihu.com/p/106276295 :重置门接近于0时,隐藏层被迫忽略之前的状态,仅用当前输入进行复位,有效地使隐藏状态丢弃将来发现的任何不相关信息;更新门控制将要有多少信息从前一个隐藏状态传递到当前隐藏状态,有助于记住长期信息
An Empirical Exploration of Recurrent Network Architectures
$z_t$是更新门,$g_t$是重置门,$s_t$是状态,$\tilde{s}_t$是对于$x_t$的候选状态
$s_t=\tilde s_t\odot z_t+(1-z_t)\odot s_{t-1}$
$M_z,N_z$是权重矩阵,$b_z$是偏差矩阵
$z_t=\sigma(M_z x_t+N_zs_{t-1}+b_z)$
$M_s,N_s$是权重矩阵,$b_s$是偏差矩阵
$\tilde{s}_t=tanh(M_sx_t+g_t\odot (N_ss_{t-1})+b_s)$
$g_t=\sigma(M_gx_t+N_gs_{t-1}+b_g)$
通过自注意力机制得到相同实体多语种描述中共享的部分
$u_t=tanh(M_as_t+b_a)$
$a_t=\frac{exp(u^Tx_t)}{\sum\limits_{x_i\in X}exp(u^T_ix_i)}$
$v_t=|X|a_tu_t$
$u_t$是$s_t$的一个隐藏表示,归一化注意力$a_t$是通过softmax计算的,测量$x_t$在对$X$编码中的重要性,应用到$u_t$上获取自注意力输出$v_t$,利用$|X|$包含长度信息
多语言词嵌入:在多语种并行语料库和单语种语料库上训练Bilbowa,训练好词向量之后固定词向量,然后放入描述编码器进行编码
使用双层堆叠GRU进行编码,利用仿射层将输入平均化$d_e=tanh(M_d(\frac 1 {|d_e|}\sum\limits_{i=1}^{|d_e|}v_i^{(2)})+b_d)$和输出相同
$S_D=\sum\limits_{(e,e')\in \{L_i,L_j\}}-LL_1-LL_2=\sum\limits_{(e,e')\in \{L_i,L_j\}}-log(P(e|e'))-log(p(e'|e))$
$LL_1=log\sigma(d_e^Td_{e'})+\sum\limits_{k=1}^{|B_d|}E_{e_k\sim U(e_k\in E_{L_i})}[log\sigma(-d_{e_k}^Td_{e'})]$
$LL_2=log\sigma(d_e^Td_{e'})+\sum\limits_{k=1}^{|B_d|}E_{e_k\sim U(e_k\in E_{L_j})}[log\sigma(-d_{e}^Td_{e_k})]$
$B_d$是ILL采样,同时负采样另一语言的所有$e_k$,除了$e$
8. Non-translational Alignment for Multi-relational Networks¶
TODO: 不全
基于TransE的方法表示能力较差,无法解决三角关系的问题,本文提出基于统计的方法
对于$v_i$,在$r_s$关系下有目标实体$v_j$的概率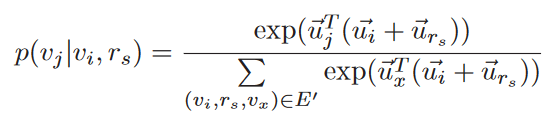
目标函数:
$\omega_{ij}$是边权重
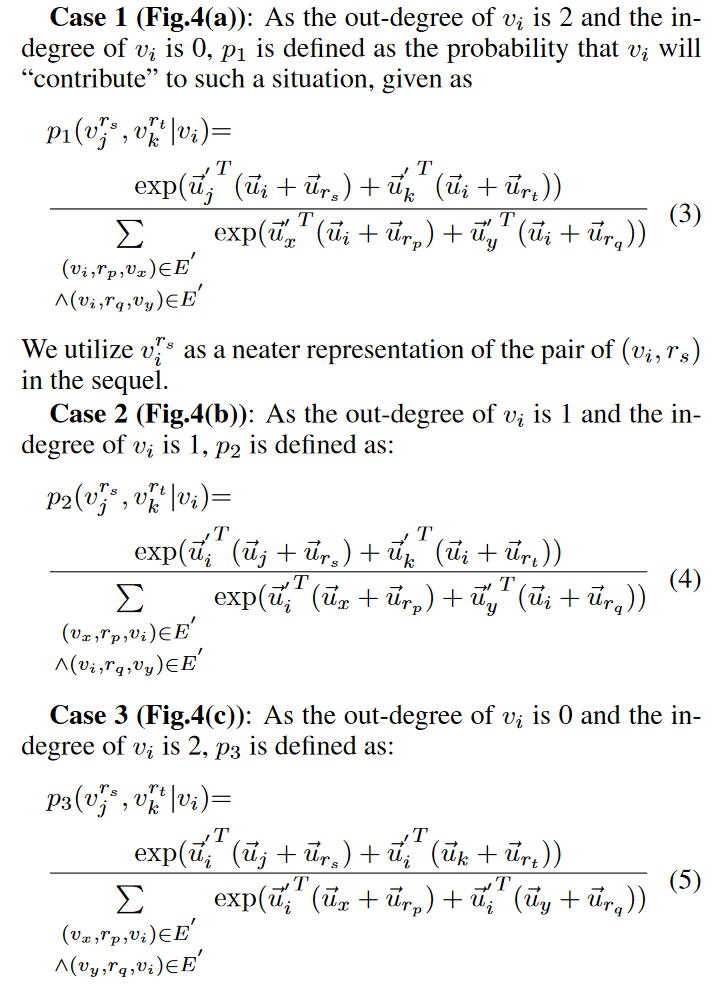
最小化目标函数可以得到嵌入
对齐目标函数:
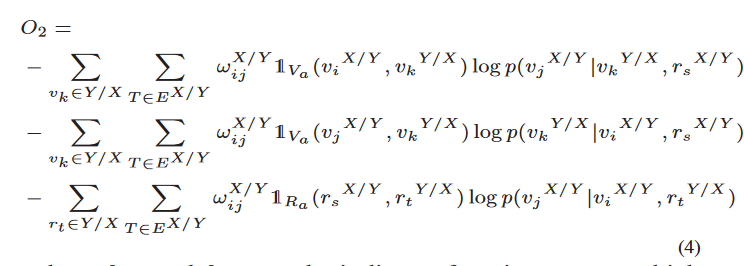
利用随机梯度下降训练模型
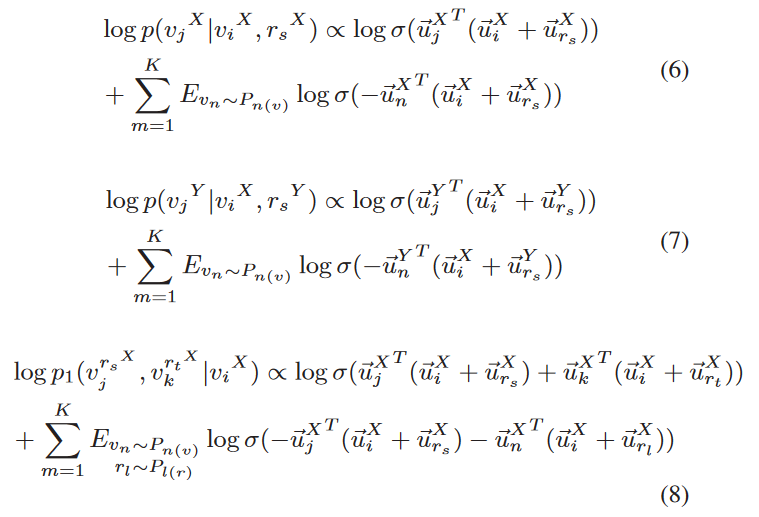
利用余弦距离确定是否对齐
9. LinkNBed: Multi-Graph Representation Learning with Entity Linkage¶
学习一系列聚合器用于提取多图中的实体和关系的上下文信息,并将信息嵌入到低维空间中。利用这些表示学习关系分数。
- 如果两个实体对齐,则它们的嵌入距离相近
- 如果两个实体对齐,则在一个三元组中替换彼此,得到三元组分数相似
原子层:如下学习嵌入:$v^*=f(W^**),*\in\{e^s,e^o,r,t\}$分别是头尾实体、关系、类型的嵌入,$v^*$是学习后的嵌入,$W^*$是嵌入矩阵,$*$是对应的one-hot码,$f$是非线性激活函数(relu)
属性是键值对,如下嵌入:$a=f(W^{key}a^{key}+W_{val}a_{val}),a_{key},a_{val}$是key的one-hot和value的特征向量
上下文层:通过聚合相关实体向量学习不同的上下文信息$c(z)=AGG(\{z',\forall z'\in C(z)\})$
- $c(z)$是聚合后的上下文信息表示,$z$是实体或关系
- $C(z)$是在$z$上下文中出现的部件,$z'$是这些部件的向量表示
- AGG是合并器,可能是Mean,Max,Pooling,LSTM
- 上下文可能有不同影响,因此利用自注意力机制$c(z)=AGG(q(z)*\{z',\forall z'\in C(z)\})$,$q(z)=\frac{exp(\theta_z)}{\sum\limits_{z'\in\{C(z)\}}exp(\theta_{z'})}$,$\theta_z's$是注意力参数
- 实体邻居上下文:$N_c(e)$也是矩阵,对于$t=(e^s,r,e^o)$,$N_c(e^s)$为和$e^s$邻近但是不是$e^o$的实体,使用随机游走获取$k$轮$l$长度范围内的邻居。利用Mean聚合器
- 实体属性上下文:$A_c(e)$,收集$e$的所有实体属性嵌入,利用Max聚合器
- 关系类型上下文:$T_c(r)$,给定一个关系$r$,目标是获取关系中实体类型的影响。通过Mean聚合$r$的类型
表示层:计算原子层和上下文层后,利用如下获取最终表示和关系

关系分数:$g(e^s,e^r,e^o)=\sigma(z^{r^T}\cdot (z^{e^s}\odot z^{e^o}))$,$\sigma$是非线性激活函数,$\odot$是逐元素乘积
模型参数空间为$\mathbf\Omega=\mathbf{\{\{W_i\}_{i=1}^5,W^E,W^R,W^{key},W^{val},W^{v},\Theta\}}$
关系学习损失:$L_{rel}=\sum\limits_{c=1}^Cmax(0,\gamma-g(e^s_p,r_p,e^o_p)+g'(e_c^s,r_p,e^o_p),e^s_c$表示破坏三元组,$g'$评估破坏三元组的分数,$$
连接度学习损失:$L_{lab}=\sum\limits_{z=1}^Zmax(0,\gamma-g(e^+_Y,r_X,e^o_X)+g'(e^-_Y,r_X,e^o_X)_z)$,知识图谱X中的三元组$(e_X^s,r_X,e_X^o)$,首先找到Y中相同的实体$e^+_Y$替换$e_X^s$计算$g$,然后从Y中寻找所有$e_X^s$的负标签集合$E^-_Y$,
联合优化以上两个损失函数,得到最终损失函数$L(\mathbf\Omega)=\sum\limits_{i=1}^N[b\cdot L_{rel}+(1-b)\cdot L_{lab}]+\lambda||\mathbf\Omega||^2_2$
使用Adam随机梯度下降训练
10. Cross-lingual Knowledge Graph Alignment via Graph Convolutional Networks¶
对齐的实体通常有相似属性并且具有相似邻居,GCN可以结合属性和邻居信息,利用GCN将实体映射到低维向量
结构和属性嵌入:$[H_s^{(l+1)};H_a^{(l+1)}]=\sigma(\hat D^{-\frac 1 2}\hat A\hat D^{-\frac 1 2}[H_s^{(l)}W_s^{(l)};H_a^{(l)}W_a^{(l)}])$
其中$W_*^{\#}$是第$\#$层权重矩阵,$\sigma=ReLU$,
利用双层GCN进行训练,每一个GCN处理一个KG并生成嵌入
由于KG中关系是有类型的,所以计算$a_{ij}\in A$
$fun(r)=\frac{\#her}{\#tr}$
$ifun(r)=\frac{\#ter}{\#tr}$
$\#her,ter,tr$分别是带有关系$r$的头实体、尾实体和三元组数量
$a_{ij}=\sum\limits_{<e_i,r,e_j>\in G}ifun(r)+\sum\limits_{<e_j,r,e_i>\in G}fun(r)+$
实体对其度使用如下计算$D(e_i,v_j)=\beta\frac{f(h_s(e_i),h_s(v_j))}{d_s}+(1-\beta)\frac{f(h_a(e_i),h_a(v_j))}{d_a}$,$d_s,d_a$是结构嵌入和属性嵌入的维度,$f$是一范数
使用随机梯度下降训练,损失函数
$L_s=\sum\limits_{(e,v)\in S}\sum\limits_{(e',v')\in S'_{(e,v)}}[f(h_s(e),h_s(v))+\gamma_s-f(h_s(e'),h_s(v'))]_+$
$L_s=\sum\limits_{(e,v)\in S}\sum\limits_{(e',v')\in S'_{(e,v)}}[f(h_a(e),h_a(v))+\gamma_a-f(h_a(e'),h_a(v'))]_+$
项目地址:https://github.com/1049451037/GCN-Align
Entity Alignment between Knowledge Graphs Using Attribute Embeddings¶
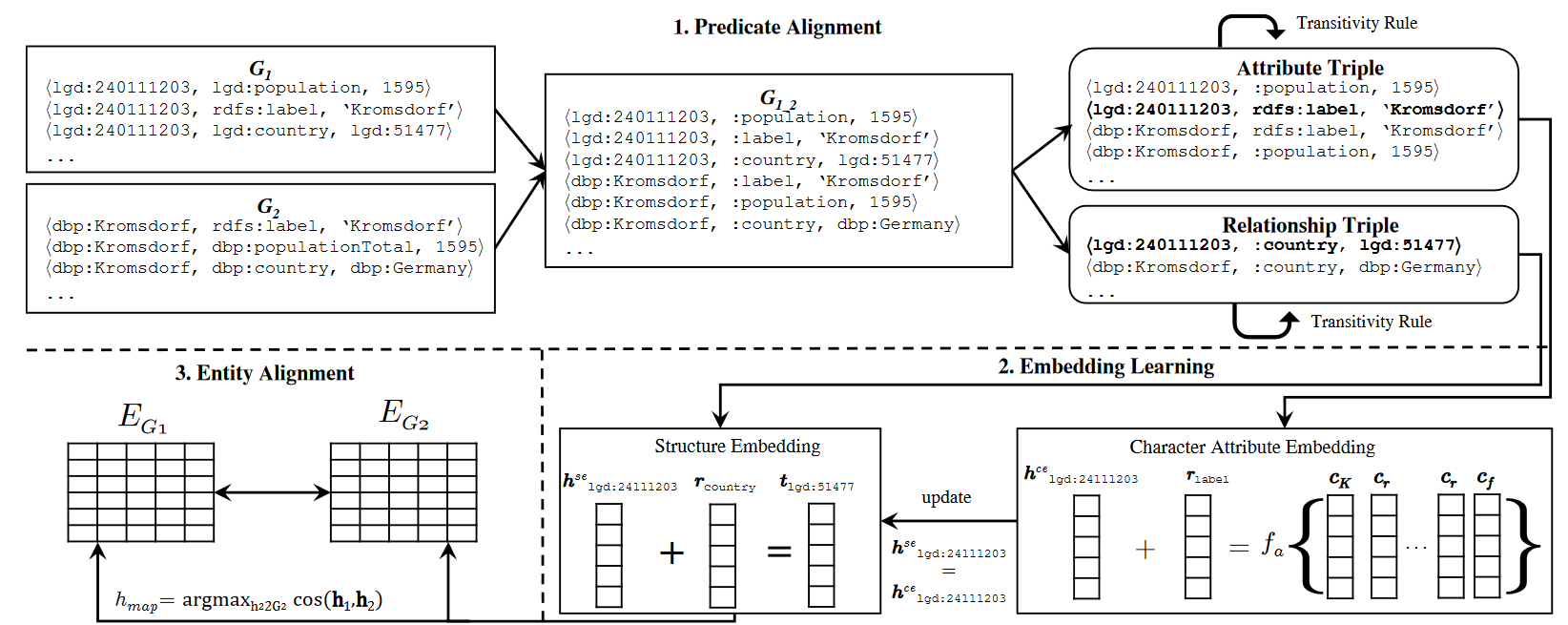
属性谓词对齐:属性谓词可能有命名转换和部分对齐,所以使用最后一部分的编辑距离进行对齐,阈值0.95
利用TransE学习结构嵌入$J_{SE}=\sum\limits_{t_r\in T_r}\sum\limits_{t_r'\in T_r'}max(0,\gamma+\alpha(f(t_r)-f(t_r')))$,$\alpha=\frac{count(r)} {|T|}$,$\alpha$用于控制从已经对齐的实体上学到更多,因为对齐的谓词比没对齐的谓词要多
属性字符嵌入: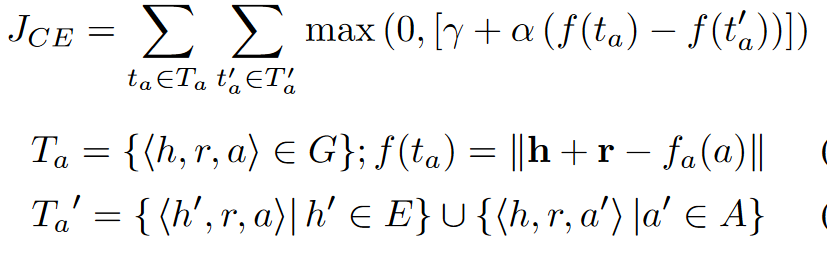
$f_a$是组合函数,包括n-gram法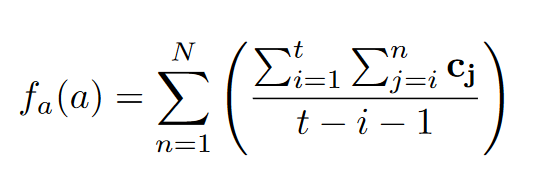 和LSTM法
和LSTM法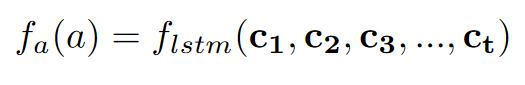
联合嵌入损失函数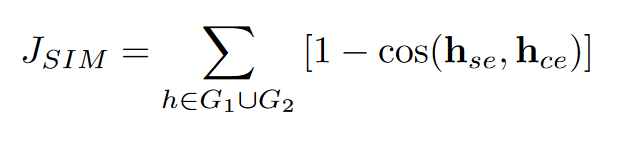
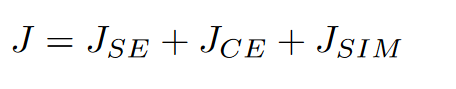
实体对齐: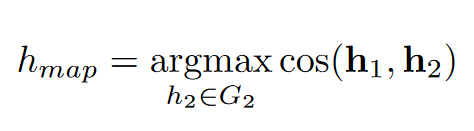
同时利用属性增强规则,即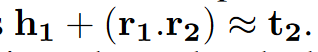
GCN-Align¶
对齐的实体通常有相似属性并且具有相似邻居,GCN可以结合属性和邻居信息,利用GCN将实体映射到低维向量
结构和属性嵌入:$[H_s^{(l+1)};H_a^{(l+1)}]=\sigma(\hat D^{-\frac 1 2}\hat A\hat D^{-\frac 1 2}[H_s^{(l)}W_s^{(l)};H_a^{(l)}W_a^{(l)}])$
其中$W_*^{\#}$是第$\#$层权重矩阵,$\sigma=ReLU$,
这里$\hat D^{-\frac 1 2}\hat A\hat D^{-\frac 1 2}$实际上计算了一个矩阵的对称归一化,$D^{0.5}$就是矩阵每一个元素都${}^{0.5}$
https://zhuanlan.zhihu.com/p/412337460
利用双层GCN进行训练,每一个GCN处理一个KG并生成嵌入

由于KG中关系是有类型的,所以计算$a_{ij}\in A$ 这个A就是上面的A,用于表示图的结构信息
$fun(r)=\frac{\#her}{\#tr}$
$ifun(r)=\frac{\#ter}{\#tr}$
$\#her,ter,tr$分别是带有关系$r$的头实体、尾实体和三元组数量
代码实现
def func(KG):
head = {} # 头实体的数量
cnt = {} # 关系的数量
for tri in KG:
if tri[1] not in cnt:
cnt[tri[1]] = 1
head[tri[1]] = set([tri[0]])
else:
cnt[tri[1]] += 1
head[tri[1]].add(tri[0])
r2f = {}
for r in cnt:
r2f[r] = len(head[r]) / cnt[r]
return r2f
def ifunc(KG):
tail = {} # 尾实体的数量
cnt = {} # 关系的数量
for tri in KG:
if tri[1] not in cnt:
cnt[tri[1]] = 1
tail[tri[1]] = set([tri[2]])
else:
cnt[tri[1]] += 1
tail[tri[1]].add(tri[2])
r2if = {}
for r in cnt:
r2if[r] = len(tail[r]) / cnt[r]
return r2if
def get_weighted_adj(e, KG):
r2f = func(KG) # r->头实体比例
r2if = ifunc(KG) # r->尾实体比例
M = {}
for tri in KG:
if tri[0] == tri[2]:
continue
if (tri[0], tri[2]) not in M:
M[(tri[0], tri[2])] = max(r2if[tri[1]], 0.3)
else:
M[(tri[0], tri[2])] += max(r2if[tri[1]], 0.3)
if (tri[2], tri[0]) not in M:
M[(tri[2], tri[0])] = max(r2f[tri[1]], 0.3)
else:
M[(tri[2], tri[0])] += max(r2f[tri[1]], 0.3)
row = []
col = []
data = []
for key in M:
row.append(key[1])
col.append(key[0])
data.append(M[key])
return sp.coo_matrix((data, (row, col)), shape=(e, e))
# ...
# 下面用于获取\hat A
adj + sp.eye(adj.shape[0])
# 然后进行一个正规化
def normalize_adj(adj):
"""Symmetrically normalize adjacency matrix."""
adj = sp.coo_matrix(adj)
rowsum = np.array(adj.sum(1)) # 每一行求和
d_inv_sqrt = np.power(rowsum, -0.5).flatten()
d_inv_sqrt[np.isinf(d_inv_sqrt)] = 0.
d_mat_inv_sqrt = sp.diags(d_inv_sqrt)
return adj.dot(d_mat_inv_sqrt).transpose().dot(d_mat_inv_sqrt).tocoo()
$a_{ij}=\sum\limits_{<e_i,r,e_j>\in G}ifun(r)+\sum\limits_{<e_j,r,e_i>\in G}fun(r)+$
实体对其度使用如下计算$D(e_i,v_j)=\beta\frac{f(h_s(e_i),h_s(v_j))}{d_s}+(1-\beta)\frac{f(h_a(e_i),h_a(v_j))}{d_a}$,$d_s,d_a$是结构嵌入和属性嵌入的维度,$f$是一范数
使用随机梯度下降训练,损失函数
$L_s=\sum\limits_{(e,v)\in S}\sum\limits_{(e',v')\in S'_{(e,v)}}[f(h_s(e),h_s(v))+\gamma_s-f(h_s(e'),h_s(v'))]_+$
$L_s=\sum\limits_{(e,v)\in S}\sum\limits_{(e',v')\in S'_{(e,v)}}[f(h_a(e),h_a(v))+\gamma_a-f(h_a(e'),h_a(v'))]_+$
代码实现
def align_loss(outlayer, ILL, gamma, k):
left = ILL[:, 0] # 源实体
right = ILL[:, 1] # 目标实体
t = len(ILL)
left_x = tf.nn.embedding_lookup(outlayer, left) # 获取left中所有实体的嵌入
right_x = tf.nn.embedding_lookup(outlayer, right) # 获取right中实体的所有嵌入
A = tf.reduce_sum(tf.abs(left_x - right_x), 1) # L1-norm
neg_left = get_placeholder_by_name("neg_left") # 获取负实体 #tf.placeholder(tf.int32, [t * k], "neg_left")
neg_right = get_placeholder_by_name("neg_right") #tf.placeholder(tf.int32, [t * k], "neg_right")
neg_l_x = tf.nn.embedding_lookup(outlayer, neg_left)
neg_r_x = tf.nn.embedding_lookup(outlayer, neg_right)
B = tf.reduce_sum(tf.abs(neg_l_x - neg_r_x), 1)
C = - tf.reshape(B, [t, k])
D = A + gamma
L1 = tf.nn.relu(tf.add(C, tf.reshape(D, [t, 1]))) # 第一对的损失值
neg_left = get_placeholder_by_name("neg2_left")# 选了第二对负实体 #tf.placeholder(tf.int32, [t * k], "neg2_left")
neg_right = get_placeholder_by_name("neg2_right") #tf.placeholder(tf.int32, [t * k], "neg2_right")
neg_l_x = tf.nn.embedding_lookup(outlayer, neg_left)
neg_r_x = tf.nn.embedding_lookup(outlayer, neg_right)
B = tf.reduce_sum(tf.abs(neg_l_x - neg_r_x), 1)
C = - tf.reshape(B, [t, k])
L2 = tf.nn.relu(tf.add(C, tf.reshape(D, [t, 1]))) # 第二对损失函数
return (tf.reduce_sum(L1) + tf.reduce_sum(L2)) / (2.0 * k * t) # 归一化
项目地址:https://github.com/1049451037/GCN-Align
实际实现还加了Dropout层
源码中发现如果有多个support($\hat D^{-\frac 1 2}\hat A\hat D^{-\frac 1 2}$)会将这些support加起来,共同起作用
(A矩阵过于单薄了吧)
环境¶
conda create -n gcn-align python==3.6
conda install cudatoolkit==9 cudnn==7.3.1 scipy==1.1.0 networkx==2.2
pip install tensorflow-gpu==1.10.1
Relation-Aware Entity Alignment for Heterogeneous Knowledge Graphs¶
Google翻译有20%的错误,会导致初始嵌入问题
将$G_1$和$G_2$放在一起,点集$V^e=E_1\cup E_2$,边集$\epsilon^e=T_1\cup T_2$,由于种子实体并未联通,所以$G_1,G_2$没有联通
首先构造对偶关系图:给定原始图 Ge,其对偶关系图 Gr = (Vr, Er) 构造如下: 1) 对于 Ge 中的每一种关系 r,在 Vr 中都会有一个顶点 vr,因此 Vr = R1 ∪R2; 2) 如果两个关系 ri 和 rj 在 Ge 中共享相同的头或尾实体,那么我们在 Gr 中创建一条边 ur ij 连接 vr i 和 vr j
$u^r_{ij}$的权重$w^r_{ij}$表示两个关系$r_i,r_j$共享的实体有多相似
对偶关系图和原始图的节点表示通过GAT获取,可以更好的让两图交互。通过堆叠多个交互来让两个图互相提升
对偶注意力层:输入:$X^r\in\mathbb R^{m\times 2d}$,每一行是一个节点的表示,$N^r_i$是$v^r_i$的邻居索引集,$\alpha^r_{ij}$是对偶注意力,$\sigma^r$是ReLU,$\eta$是Leaky ReLU,$a^r$是一个2d全连接层,可以将$2d'$维的输入映射到常数,$c_i$是从之前的原始注意力层获取的关系$r_i$的关系表示,$\tilde\mathbf x^r$是点$v^r_i$的输出表示
在基于嵌入的框架中,关系表示无法直接提供,因此结合原始图中平均后的头和尾实体表示关系。当是第一层对偶关系层时,相关参数通过初始化获取
原始图GAT利用对偶关系表示计算节点嵌入。输入$X^e\in\mathbb R^{n\times d}$。对于实体$e_q$,$x^r_{qt}$是从实体$q$通过关系$r$到$t$中$r$的表示,$N^e_q$是邻居索引
初始嵌入使用词嵌入表示,将初始嵌入混合到输出中用于添加词嵌入信息
利用双层GCN捕捉更深远的邻居结构
并且GCN之前使用门控网络用于抑制噪声积累和保留有用的信息
对齐是使用距离
训练的损失函数如下,$\mathbb L$是种子,$\mathbb L'$是破坏的种子对。破坏种子对不是随机选,而是根据距离随机选k个最近的非对齐种子
项目地址:https://github.com/StephanieWyt/RDGCN
RAGA: Relation-aware Graph Attention Networks for Global Entity Alignment¶
包含4层,基础邻居合并层、关系感知的图注意力网络、端到端训练、全局对齐算法
基础邻居合并层,由门控图卷积神经网络构成,但是去掉了权重矩阵$W^{(l)}$
关系感知的图注意力网络
由于关系的分布比实体的分布更致密,关系表示应该有不同的信息量并且有不同的信息空间。对实体嵌入应用一个线性转换,然后利用注意力权重计算关系嵌入。利用连接的头实体和尾实体,和RDGCN不同,不忽略实体关系双连接,用于调整注意力权重
关系嵌入如下
上式表示的是关系k相对于头实体$h$的嵌入,相对于尾实体t的嵌入计算方法相同。最终的关系表示如下
关系感知的实体表示:根据经验,一个实体的邻居关系更能够精确表示自身,因此将近邻关系重新分组到实体表示中,特定的,对于实体$e_i$,计算外向嵌入(作为头实体)和内向嵌入(作为尾实体)
增强实体表示:在关系感知实体表示中,实体感知了一跳实体,为了加强2跳实体的影响,增加一层一般GAT来获取增强实体表示,考虑双向边并且不包含线性转换矩阵
因为$N_i$是邻居实体集合,邻居包含两跳的关系,所以这里就利用了两跳的关系
端到端训练
使用曼哈顿距离表示两个实体的相似度
损失函数如下,训练时随机采样k个最近的负样本。对于KG中的每一个三元组都认为是正样本
全局对齐算法:实体的局部对齐会导致多对一的问题并且降低性能并且带来歧义,使用微调相似度代替原来的相似度。使用DAA算法对齐(Collective Embedding-based Entity Alignment via Adaptive Features)
在第一轮中,每个源实体向它最喜欢的目标实体提出建议,然后目标实体与它目前最喜欢的源实体临时匹配,同样,该源实体与目标实体临时匹配
在随后的每一轮中,每个未匹配的源实体向它尚未提议的最优选的目标实体提出建议(无论目标实体是否已经匹配),然后每个目标实体如果当前不匹配则接受提议 或者如果它更喜欢新的提议者而不是它当前的匹配(在这种情况下,它拒绝它的临时匹配并且变得不匹配)。
环境¶
创建环境conda create -n raga
激活环境conda activate raga
安装torch conda install pytorch torchvision torchaudio pytorch-cuda=11.6 -c pytorch -c nvidia 目前网速较慢,需要提高网速可以下载对应文件之后搭建稳定的本地镜像源
然后编译安装apex,就很麻烦
首先安装cuda-nvprof,这个包提供cuda_profiler_api.h头文件,注意版本和conda list列出的cuda-toolkit版本相同
conda install -c "nvidia/label/cuda-11.6.2" cuda-nvprof
clone代码并编译,这里可以提前安装ninja提高编译速度
pip install packaging && git clone https://github.com/NVIDIA/apex.git && cd apex && pip install -v --disable-pip-version-check --no-cache-dir --global-option="--cpp_ext" --global-option="--cuda_ext" ./
安装另外两个包conda install pytorch-sparse -c pyg,pip install torch_geometric
导出环境 conda env export > RAGA_conda.yml
导入 conda env create -f RAGA_conda.yml
参考自:https://github.com/PaddlePaddle/Paddle/issues/45929
Multi-information embedding based entity alignment¶
三元组嵌入:TransE
,其中S是两个KG的三元组
其中破坏的三元组通过随机替换头实体和尾实体构成
将两个知识库嵌入到同一向量空间,M是种子实体,R是对齐可靠性。如果是种子实体,则可靠性为1,否则是语义距离
最终损失函数:
邻居信息嵌入:
前向、反向邻居如下所示:
通过加权表示计算邻居对于实体本身的影响。对于每一个前向邻居,如下学习向量表示:拼接$e_i,r_i$的向量,然后使用全连接层进行学习。f=tanh
$w_i$用于衡量$e_i,r_i$对于实体的重要性,有三方面指标
- 映射基数:可能是1-1或1-n,对于前向邻居$E$,如果是$|E|==1$,则是1-1,否则1-n,n=$|E|$。映射基数不同,每个节点重要性也不同。所以基于映射基数的权重设置为
- 关系关联度:包括$r_i$和其它邻居中关系的关联度。关系的关联度如下表示:
,$\psi(x)=1,x=true$,否则为0;两个KG之间的关系也有关联度,
。基于以上两个关联度,总关联度为
。关系的本KG关联度越高,说明本身的独特性越低,可以被其它关系取代;但是KG'关联度高,说明可以帮助嵌入
- 注意力机制:以上两种权重方法没有考虑到向量表示中的信息,
,最终权重
,
邻居嵌入
邻居嵌入损失函数
训练算法
实体对齐
利用阈值$\theta_{tn}$来确定是否对齐
Embedding-Based Entity Alignment Using Relation Structural Similarity¶
关系相似度:
实体相似度直接使用曼哈顿距离
参数交换:即交换已经对齐的实体,形成新的三元组,增加训练数据
采用自对抗负采样,先均匀负采样,然后计算每一个负样本的权重,
使用优化TransE进行训练,优化损失函数:,Adam优化器
训练:
- 利用关系相似度确定关系是否对齐
- 利用已经对齐的实体和关系(包括利用关系分数对齐的)生成新的三元组,此时两个知识图谱合并成了一个。这里采用参数交换的方法,即替换已经对齐的头尾实体生成新的三元组
- 利用新的知识图谱学习嵌入(TransE)
- 对于负采样给一个权重,权重由实体嵌入之间的距离表示
- 新的损失函数
Neighborhood Matching Network for Entity Alignment¶
结构嵌入:将两个KG合并成一个,输入
$\varepsilon$是归一化常量,$N_i$是$i$的邻居
利用高速门控网络控制噪声传播
邻居采样:并不是所有的一跳邻居都对对齐有利,所以进行一个下采样
给定一个实体$e_i$,采样1跳邻居$e_{i\_j}$的概率是,$W_s$是共享权重矩阵。GCN学习的实体信息包含丰富的上下文信息,包括邻居信息和实体语义信息。某个邻居在上下文上越多的关联中心实体$e_i$,就更有可能被采样。对等实体在现实世界中也可能有相似上下文,所以邻居和中心实体越有关联,就能为对齐提供越多线索。
邻居匹配:对于实体$e_i$,需要比较取样后的邻居子图,选择最优的对齐实体。
由于子图数量巨大,全部进行匹配计算量过大,所以进行采样,计算两个实体之间的相似度进行匹配
实体$i$的邻居$p$的跨图匹配向量为,$m_p$衡量了另一个子图中最近邻居和当前实体的距离,然后拼接邻居和带有权重的匹配向量
这种注意力机制能够精确检测另一子图的哪一个邻居最能匹配目标邻居
邻居合并:结合邻居连接信息生成用于对齐的最终嵌入。对于实体$e_i$,首先合并取样后的邻居$\{\hat h_p\}$,然后计算邻居表示
然后结合$h_i$和$g_i$表示实体
利用两个实体的距离判断是否应该对齐
损失函数
预训练之后,将损失函数替换成
取样是不可微分的,因此不是直接采样,而是通过直观加权求和聚合所有信息
采样方式相对简单
- 利用邻居信息反映实体信息
- 候选实体对相互给出邻居注意力
- 对邻居进行采样减少计算量
Dual Gated Graph Attention Networks with Dynamic Iterative Training for Cross-Lingual Entity Alignment¶
KG内注意力:用于学习单语种KG内部特征
其中$M_1^l,M_2^l$是正规化的注意力指标,$W^l$是转换参数,$\sigma$是激活函数,$E^l$是第$l$层的嵌入
$M_1^l$如下计算
$s^l_{(i,j)}$是$i->j$实体的注意力
$N_{e_i}$是$e_i$实体的邻居,$v$是注意力向量
跨KG注意力,设$A_{ctx}$是上下文对齐
$\delta=1e-8$是平滑因子,$c_{i,j}$是$e_i\in E_1,e_j\in E_2$的注意力
跨知识图谱特征可以如下计算
利用门控机制权衡知识图谱内部和跨知识图谱特征
$\theta$是sigmod
实际中堆叠$L$层注意力机制
优化和预测:利用$A_{ctx}$作为输入,$A_{obj}$作为目标进行训练
$e_1^-$是负实体,$D$使用L1损失
利用迭代策略:只有当$e_i,e_j$互为最近的实体时,才加入种子实体。
注意力如下更新
损失函数也会更新
- 利用内部注意力机制学习单KG内部特征
- 利用KG间注意力机制学习种子实体中的特征
- 一部分训练集用于提供注意力,一部分训练集用于调整嵌入
- 利用保守的迭代策略添加新生成的种子,并更新注意力
Coordinated Reasoning for Cross-Lingual Knowledge Graph Alignment¶
本篇文章注意到了实体对齐之间的置信度不同和难易不同
easy-hard解码:
这里哈佛大学的对齐要比乔治·布什的对齐要简单很多,因为George W. Bush和George H. W. Bush只有毕业学校不同,因此非常用以对齐错误(用例学习)
在解码阶段迭代地应用如下步骤:
- 利用对齐模块预测所有测试集中的源实体
- 利用预定义的概率阈值$\alpha$提炼这些对齐,带有概率高于$\alpha$的对齐认为是easy的,否则认为是hard
- 如果有超过$K$个easy对齐找到,利用这些easy对齐作为额外知识来帮助剩余实体对齐,否则返回所有对齐
将这种方法应用于已有方法
已有方法模型:RDGCN
- 输入表示层:利用GCN学习实体嵌入
- 节点级匹配层:通过比较两个KG的实体嵌入捕获局部信息
- 图级匹配层:利用另一个GCN将局部匹配信息传播到整个图,通过Pooling生成固定长度的图表示
- 预测层:应用前馈神经网络计算固定长度的图表示,并应用softmax
本文增强模型:
- 加强表示层:easy对齐中的实体对应该具有相同嵌入
- 强化节点级匹配层:强制让已经对齐节点的相似度为1,然后将结果输入图级匹配层
联合实体对齐:
目标是找到最佳匹配
但是复杂度比较高,所以利用一对一约束先转化一下,这样就变成了[Agent-task Assignment Problem](https://en.wikipedia.org/wiki/Assignment problem)。Hungarian algorithm用于解决这个问题
- 找到每一行中最小值并且从其它行减去这个最小值
- 找到每一列的最小值并从其它列减去这个值
- 使用最少数量的水平线和垂直线覆盖矩阵中的所有0,如果少于n行,则转4,否则找到解
- 找到没有被覆盖的最小值v,将v从所有没被覆盖的值减去,并且将v加到被两条线覆盖的值上,回到3
算法复杂度依然有$O(N^4)$,将整个空间分成若干子空间,利用预定义阈值$\tau$丢弃候选对齐,只有两个实体共享多个相似候选时才选,因为一个大KG经常包含多个域。
- 考虑到了实体之间的不同以及对齐难易不同,利用容易对齐的实体对齐难以对齐的实体
- 充分利用训练集
- 将实体匹配问题转化为agent/task问题,得到全局最优匹配,并通过域分割缩减算法复杂度
Reinforcement Learning based Collective Entity Alignment with Adaptive Features¶
特征提取:
结构信息:GCN
利用随机梯度下降优化
语义信息:利用实体名称的平均词嵌入,词嵌入相似的实体会放在彼此附近 $N$
字符串信息:在单语种或相似多语种表示时很有用,利用Levenshtein distance $M^l
自适应特征融合:
距离测量:Bray-Curtis dissimilarity
嵌入实体:$Z$,结构相似度矩阵$M^S$,语义相似度矩阵$N$
特征融合:
- 可信实体对生成:利用之前的特征作为输入,利用特征p衡量实体ij之间的关系为$M^p_{ij}$,如果$M^p_{ij}$是行列中最大的,则实体ij就是p的可信实体对
- 对应权重计算:如果一对可信对应被q个特征生成,则权重为$1/q$,因为出现的越频繁,表示所含信息量越少;对于一个带有很大相似度的实体对,将相似度设置为一个较小的值。这种情况下非常有效的特征就不会有特别大的权重,不是那么有效的特征也可以参与对齐
- 特征权重计算:特征p的权重是从特征中获得的实体对的权重之和,除以实体对数量
- 特征融合自适应权重:融合特征相似度矩阵和自适应权重生成融合特征矩阵$M$
基于强化学习(RL)的实体对齐:
EA--序列决策问题:利用Advantage Actor-Critic模型作为强化学习决策。因为EA问题就是对于每一个源实体,决策哪个目标实体匹配,根据之前的匹配和当前状态进行决策。
- RL网络以当前状态作为输入,并给出一个action(目标实体),影响接下来的状态并得到奖励
- 以当前状态、下一状态和奖励作为输入,计算差别错误并更新网络
- 环境:源实体、目标实体、KG的邻接矩阵、融合特征矩阵M
- 状态:$s=s^1\cdot s^2+s^3$,分别是局部相似度向量(从M中获取,衡量源实体和候选实体的相似度)、排他性向量(由1和-1组成,如果某个目标实体选择,则设置为-1,否则为1)、和一致性向量(目前候选目标和之前候选目标的关联度,首先检索源KG邻接矩阵中与源实体相关的实体,这些相关实体的目标实体称为上下文实体。对于每一个候选目标实体,在KG中候选实体连接上下文实体的数量为一致性分数)
- 动作:利用一个全连接层+softmax执行选择动作
,
,即为各个动作的概率,只选最有可能执行的几个
- 奖励:不推荐之前执行过的工作,最大化局部相似度和全局一致性,第i步的奖励为
- Critic模型:因为奖励只能在每一个epoch完成之后才计算,无法实时更新。该模型依然是两层全连接层
,
,
优化学习过程:
目标是取得最大全局奖励,
如果两个实体互相认为是最高可能的实体,则认为他们大概率是对齐实体
- 利用多方面信息,包括语义信息(词嵌入)、结构信息(GCN)、字符串信息
- 利用强化学习进行实体对齐
MCEA: A multiscale convolutional gragh network using only structural information for entity alignment¶
- 多尺度卷积网络
拥有更多邻居的节点称为关键节点,但是长尾实体(邻居数量少)比例更高,这些实体带有的对齐信息是有限的
对于长尾实体使用更大卷积核,因此可以收集到更多跳的信息,长尾实体也可以积累更多信息。迭代过程中这些信息也会传给非长尾实体,方便实体对齐
- 基于半监督学习的负采样
对于某个实体,随机选择相似度列表中第二和第15个实体作为负样本,当对齐算法精度足够时,也可以保证选择的负样本有最大可能不是正确对齐的样本
- 对齐策略
利用stable marriage algorithm(SMA),这个算法更关注全局而不是贪心,这个机制保证发生错误的时候至少有两对错误,这让SMA可以更改某一个基于确实错误匹配对的高精确度错误匹配实体对,但是SMA只能匹配单个,所以只能计算Hit@1
- 形式化表述
输入:实体嵌入和关系嵌入,$N_e,N_r$是实体和关系集合,使用Heinitializer初始化。利用RREA中提出了微分关系和等距变换两个准则,利用$W_{rk}$作为图嵌入模型中关系r的第k条边的变换操作矩阵
,$W_{rk}$可以保证变换中实体的相对距离不变
图嵌入模型:
$r_k$代表$e_i,e_j$的第k条边,$N_{e_i}$是$e_i$的邻居集合
$\oplus$是向量拼接
如果$e_i$是长尾实体,只有$e_j$邻居,但是$e_j$不是长尾实体,则$e_i$如下嵌入
$\alpha_{jmo}$为注意力,如上$\alpha$计算
则嵌入是各个注意力相加
再结合关系嵌入
负采样损失函数
dist为曼哈顿距离
SMA算法
- 对于长尾实体特殊对待,让它包含更多信息
- 节点嵌入中包含节点嵌入和关系嵌入信息
- 负采样利用2到15个最相似的随机挑选
- 利用SMA算法实现实体匹配
RNM: Relation-Aware Neighborhood Matching Model for Entity Alignment¶
实体嵌入:GCN,利用预训练词嵌入初始化实体嵌入,利用高速门控网络控制噪声传播,利用L1范式计算实体间的距离
实体嵌入损失函数:
关系嵌入:利用头尾实体嵌入表示,$g^h_r,g^t_r$表示所有头尾实体嵌入的平均
根据TransE正规化:
目标函数:
关系感知的邻居匹配:
如果两个KG中的实体对齐了,则具有相同意义的关系,两个尾实体对齐的概率能够通过根据关系属性推断出来。对于每一个一跳邻居,不仅考虑连接的实体,还考虑关系,对于邻居关系对齐,考虑所有实体对和连接的关系对$C_{ij}^e=\{(n_1,n_2),(r_1,r_2)|n_1\in N_{e_i},n_2\in N_{e_{j'}},(e_i,r_1,n_1)\in T_1,(e_{j'},r_2,n_2\in T_2\}$
因此匹配集$M^e_{ij}$是$C^e_{ij}$的子集,还需要满足$(n_1,n_2)\in\mathbb L_e$,$(r_1,r_2)\in\mathbb L_r$
基于$(r_1,r_2),(n_1,n_2)$映射的概率是
则距离可以更新为
实体感知的关系匹配:
给定关系对之后,需要先获取$M^r_{ij}\subseteq C^r_{ij}=\{(h_1,h_2),(t_1,t_2)|(h_1,t_1)\in S_{r_i},(h_2,t_2)\in S_{r_{j'}}\}$
关系对的距离可以如下更新
迭代策略:$D^e,D^r$是实体和关系距离矩阵,如下初始化
- 使用确信度更高的邻居方式:不仅使用一跳邻居信息,还使用对应的关系帮助对齐
- 对于关系距离也考虑头尾实体,其实也是利用头尾实体作为邻居信息
Entity Alignment Between Knowledge Graphs Using Entity Type Matching¶
知识嵌入模块:TransE
嵌入空间对齐模块:利用MTransE的LinearTransformation
利用种子实体学习对齐矩阵
实体类型匹配模型:对于实体类型$z$,定义$S_z$为具有$z$类型的实体
$e\propto z$表示$e$具有类型$z$,利用$S_z$作为输入,输出一个向量$z_e$表示该类型的嵌入,$\sigma$是LeakyReLU
依然是利用种子实体学习类型嵌入
然后可以利用类型和实体相似度得到最终距离
对齐方式:,并且利用阈值判断是否对齐
损失函数
利用迭代训练:对于迭代中冲突的实体$e_x,e_y$都和$e_1$距离最小,如下选择两个实体
- 提取了类型信息作为辅助,帮助实体对齐
Relation-based multi-type aware knowledge graph embedding¶
和一般的定义不同,包含一个类型树,
是关系的域
实体关系嵌入层:
聚合实体本身和邻居信息
不同关系连接的邻居需要不同的权重,将同一实体的邻居按关系不同分组,并聚合组内邻居,在关系r下给一个权重(注意力),$\sigma=LeakyReLU$
对于实体$v$,和关系$r$连接的邻居$e$带来的注意力如下,$t_*$是类型嵌入
,同一关系下计算注意力的DNN是共享的,因为相同的关系下经常有相似的pattern
对注意力使用softmax
利用多头注意力得到邻居嵌入
然后融合各个邻居的嵌入
多类型嵌入层:
这里如果不是使用分类树,而是使用分类图
利用双向Transformer进行训练,每个类型的叶子节点经过双向Transformer之后就会称为嵌入
给定一个实体,它的多类型嵌入为,其中$t_i$是类型嵌入,
$\lambda$
对于三元组$<e_i,r_{ij},e_g>$
给定关系$e_i$,类型$t^{e_i}_j$的重要性为
$\Phi(D^i_{r_{ij}},t^{e_i}_j)=1$,当关系$t^{e_i}_j$在$D^i_{r_{ij}}$的域中时
然后进行一个融合
目标函数
Deep Reinforcement Learning for Entity Alignment¶
Agent:
状态:由环境给出,$s=[e_x,e_y]$其中包含对应的嵌入,邻居$N_x,N_y$,$e_y$的对手实体嵌入集$O_y$,距离$e_x$最近的k个实体,除$e_y$外,称为对手实体,这些实体可以提供额外信息
动作:一个二进制数,表示Agent的选择,因为二进制选择复杂度低,并且由纠正机会。
策略:给定一个状态,首先通过GCN提取特征
其中$c_x$是归一化常数
然后使用一个线性层组合$g_x,g_y$
并且利用互信息衡量实体间的距离,利用神经函数衡量密度比
并且利用对手实体作为负样本计算互信息
最后连接状态和动作,$p_{e_x,e_y}$是归一化的动作分布
奖励:,agent的目标是获取所有最大奖励
优化:第i步的梯度是
其中$\delta$是$\alpha$和基线相比超出多少,例如利用随机作为基线
其中G基于未来的奖励返回,T表示epoch的长度
环境:包括依赖、动态和难度
依赖:对于序列匹配,一个正确的match不仅得到一个实体对,并且排除了似乎正确的,会有更高的全局分数;即使是错误的匹配,也过滤掉了错误的实体。
连接$e_x$和它的所有实体$[e_x,e_1],[e_x,e_2],...,[e_x,e_k]$,环境维护一个序列$c1,...,c_j$,包含这样的实体对序列。一旦Agent输出动作1,所有包含$e_x,e_y$的实体对都要移除
动态:动态环境有利于Agent捕获到游戏的一般法则,防止过拟合。设置一个跳过率$p_s$,以$p_s$的概率随机跳过一个候选
难度:将难的任务打碎成几个epoch,难度可以利用两个实体余弦距离($C$)和对应的label计算,$e_{max}$是和$e_x$最近的实体距离,l=1时,如果距离差别大,则难度大
基于难度升序排列候选对,则Agent总是从相对简单的开始尝试
但是无法应用于测试集,所以利用课程学习策略
基于余弦距离排序并且基于归一化的难度分数重新设置$p_s$,因此Agent就可以从更相似的候选对开始,并且难度比较高的实体对就会有很大概率被跳过。然后逐渐减小$p_s$来近似测试集
第$t$轮的$p_s$为
$p_s^{min}$是最小跳过率,$\eta$是折现因子,呈指数增长,$d_i$是状态$i$的难度
Semi-Supervised Entity Alignment via Knowledge Graph Embedding with Awareness of Degree Difference¶
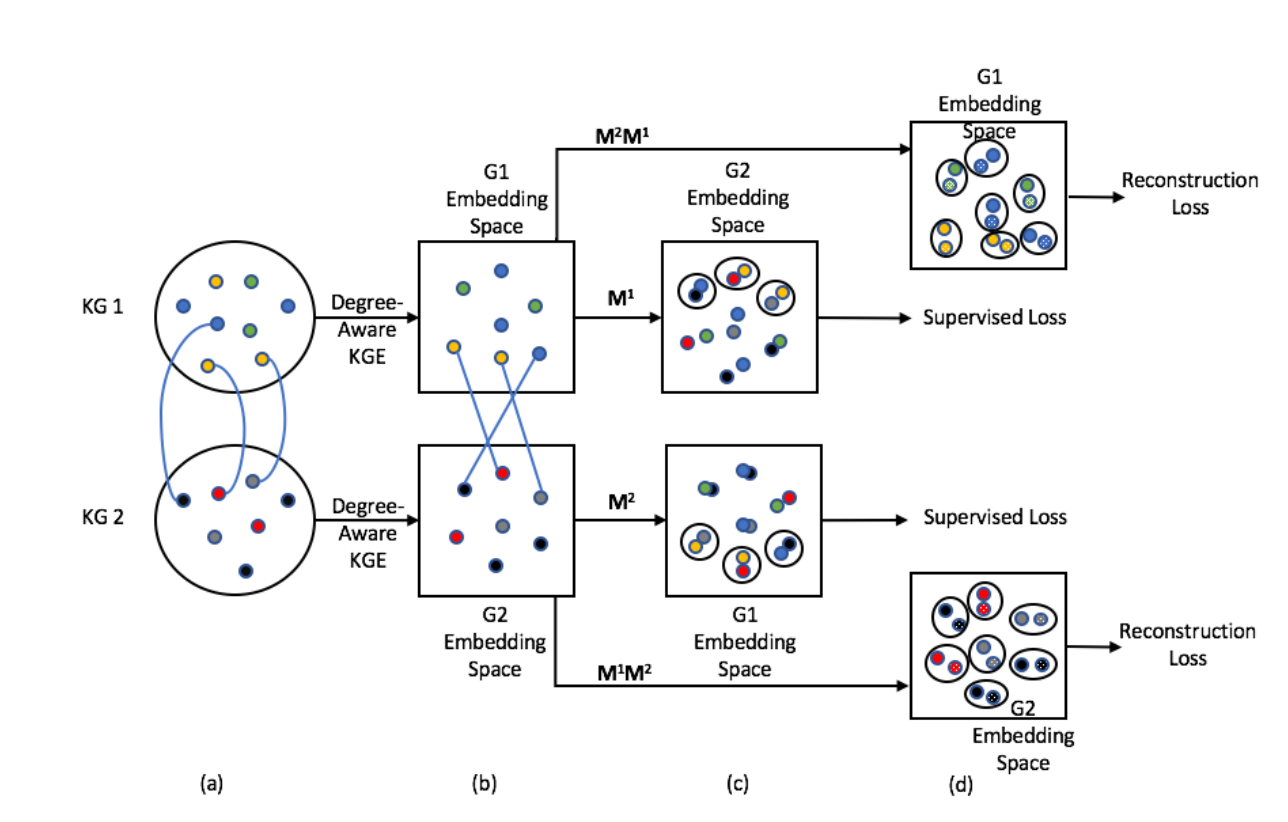
嵌入:TransE,也可以其它
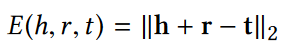
度感知的KGE方法:给定一个图$G_i$,设置两个判别器来区分不同度的实体。度感知的KGE模型视为生成器。
将实体度分成高、正常、第三类,$D_1$判别高和正常度,$D_2$判别低度。训练目标就是让判别器无法根据度信息区分实体
判别器损失函数为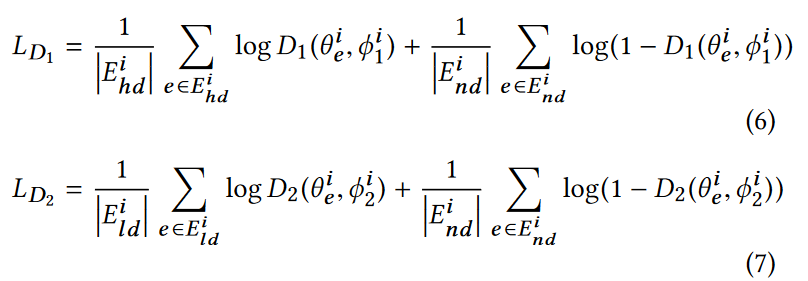
目标函数为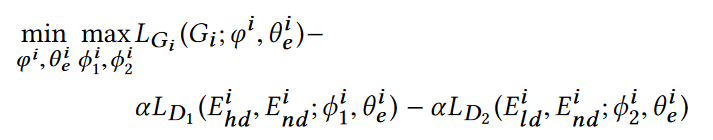
半监督实体对齐: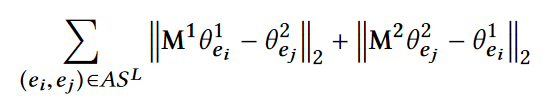
利用了CycleGAN的概念,M应该具有性质:
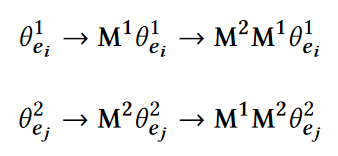
损失函数为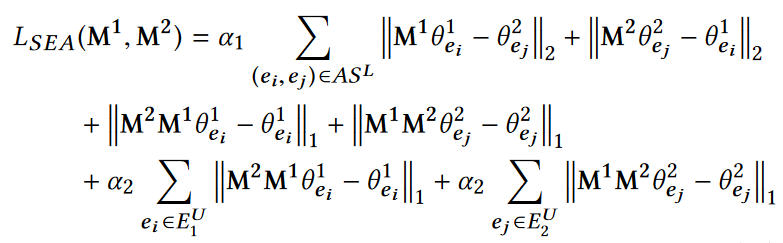
- 利用GAN排除度对于实体对齐的干扰
- 利用CycleGAN进行实体对齐,训练更好的对齐矩阵
LightEA: A Scalable, Robust, and Interpretable Entity Alignment Framework via Three-view Label Propagation¶
- 随机本体标签生成
- 三视图标签传播
- 稀疏Sinkhorn迭代
随机本体标签生成:从人脸识别中借鉴一个思路,将每一对预对齐的实体看作一类
令$(e_i,e_j)\in P$是第$x$对预对齐实体对,输入矩阵如下初始化

但是这种初始化方式会导致初始输入矩阵非常大并且非常稀疏
引理:
也就是说,d足够大时,两个随机初始化的向量近似正交。所以随机初始化可以近似独热码
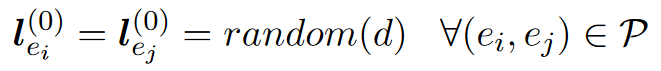
LP(标签传播)传播标签,GCN传播特征。由于随机初始化近似独特码标签,所以二者等价。
三视图标签传播:由于LP和GCN都是为同构图设计,而知识图谱是异构的,解决方法是正规化
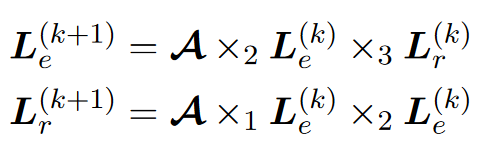
$\times_i$代表第i维相乘,但是这种方法复杂度较高,且已有的机器学习库不支持稀疏矩阵的张量相乘
将邻接张量$A$分别压缩到三视图,分别得到头尾实体、头实体-关系、尾实体-关系的关系
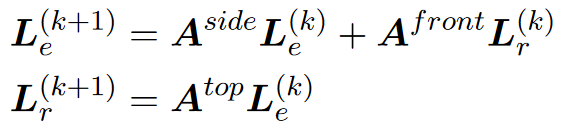
将三元组传播的过程转换成三角过程,每一个三元组的面代表一个不同视图,这种情况下标签就能在KG中有效传播,并且保留复杂度一致性。
对于每一个实体$e_i$,连接标签输出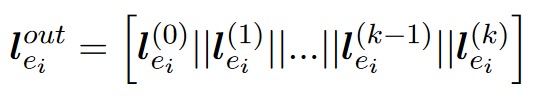
稀疏Sinkhorn迭代:
将实体匹配过程转化成任务调度过程
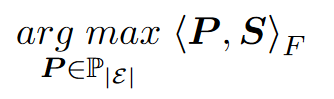
使用Sinkhorn迭代近似解决可以降低复杂度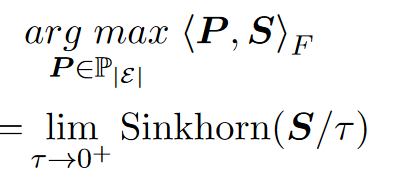
移除较小值,进一步降低复杂度
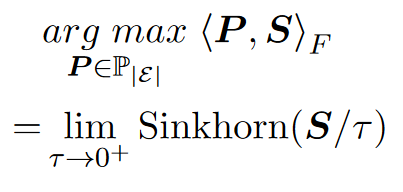
Multi-modal Contrastive Representation Learning for Entity Alignment¶
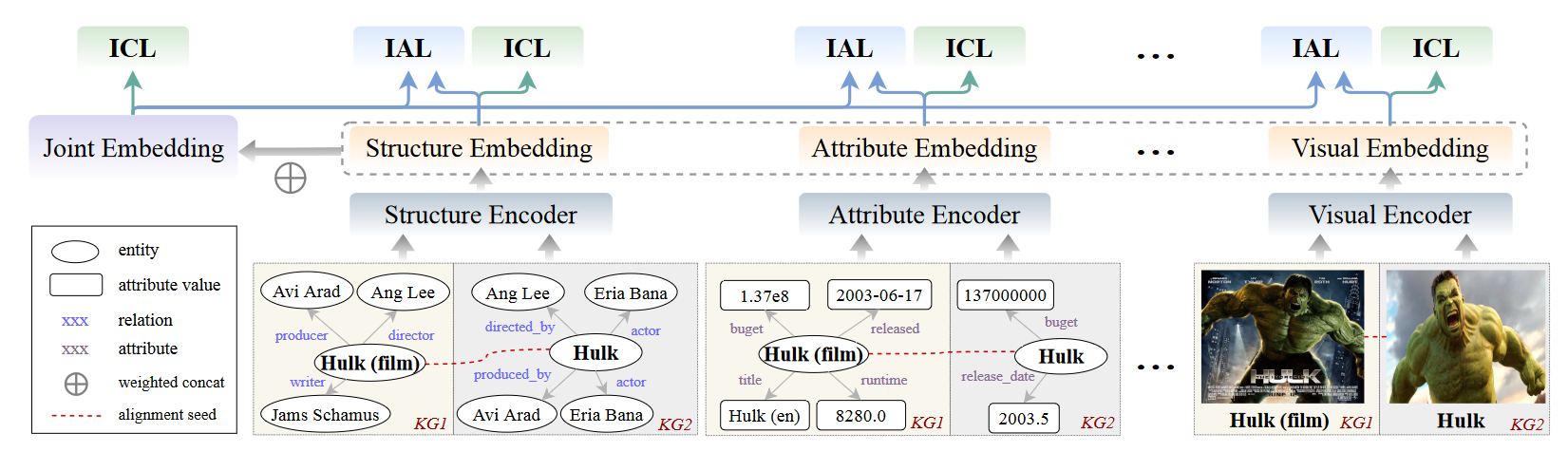
多模态嵌入:邻居结构、关系、属性、名称图像分别嵌入,然后利用简单的权重相加
邻居嵌入:利用GAT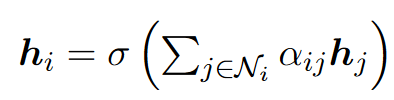
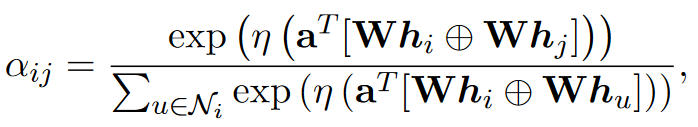
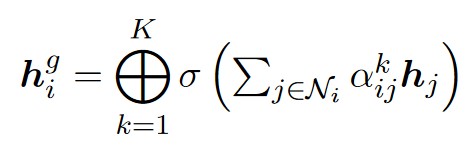 利用双层GAT
利用双层GAT
关系、属性、名称嵌入: $u_i^a,u_i^r$是bag-of-words属性和关系信息,$u_i^n$是GloVe信息
$u_i^a,u_i^r$是bag-of-words属性和关系信息,$u_i^n$是GloVe信息
利用ResNet实现图像嵌入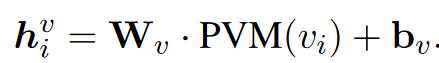
嵌入通过如下方式组合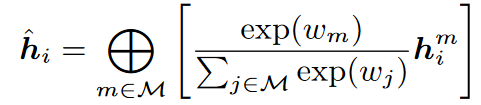
$M\in\{g,r,a,n,v\}$
模态内损失函数:利用模态内对比损失。利用同知识图谱负实体对和跨知识图谱负实体对约束嵌入空间
定义模态m的对齐概率分布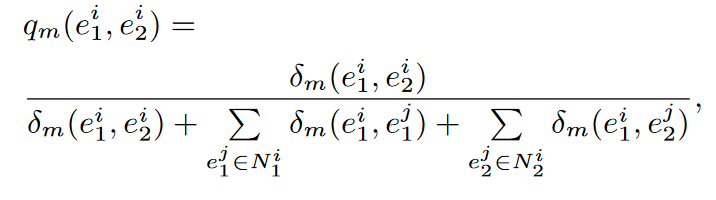
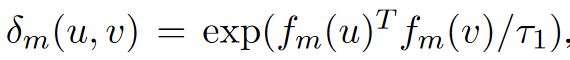 ,$f_m()$是编码器,$\tau_1$是温度。输入需要L2正规化
,$f_m()$是编码器,$\tau_1$是温度。输入需要L2正规化
ICL为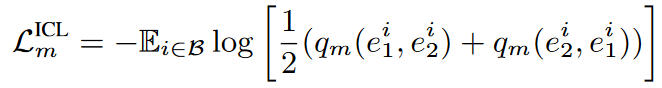
跨模态对齐损失(IAL):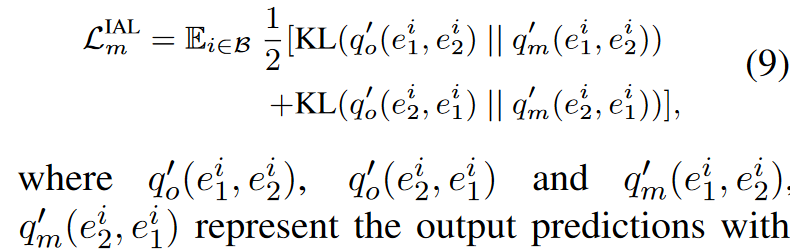 q*是模态m的单模态嵌入。通过
q*是模态m的单模态嵌入。通过 。并且利用知识蒸馏将多模态知识提取到单模态
。并且利用知识蒸馏将多模态知识提取到单模态
总体损失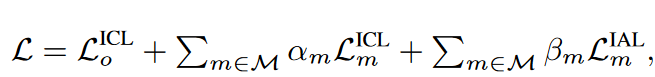 但是超参数很难交互,
但是超参数很难交互,
重写为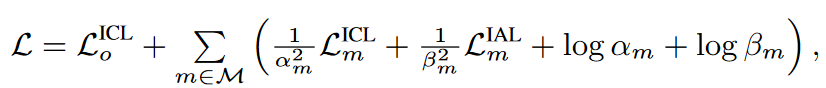 $\alpha_m,\beta_m$是可以训练的参数
$\alpha_m,\beta_m$是可以训练的参数
利用双向迭代策略在训练过程中动态添加种子
项目地址:https://github.com/lzxlin/MCLEA
- 利用大量特征融合尽可能多的信息
- 利用损失函数融合多个特征
- 利用知识蒸馏提取特征
Revisiting Embedding-based Entity Alignment: A Robust and Adaptive Method¶
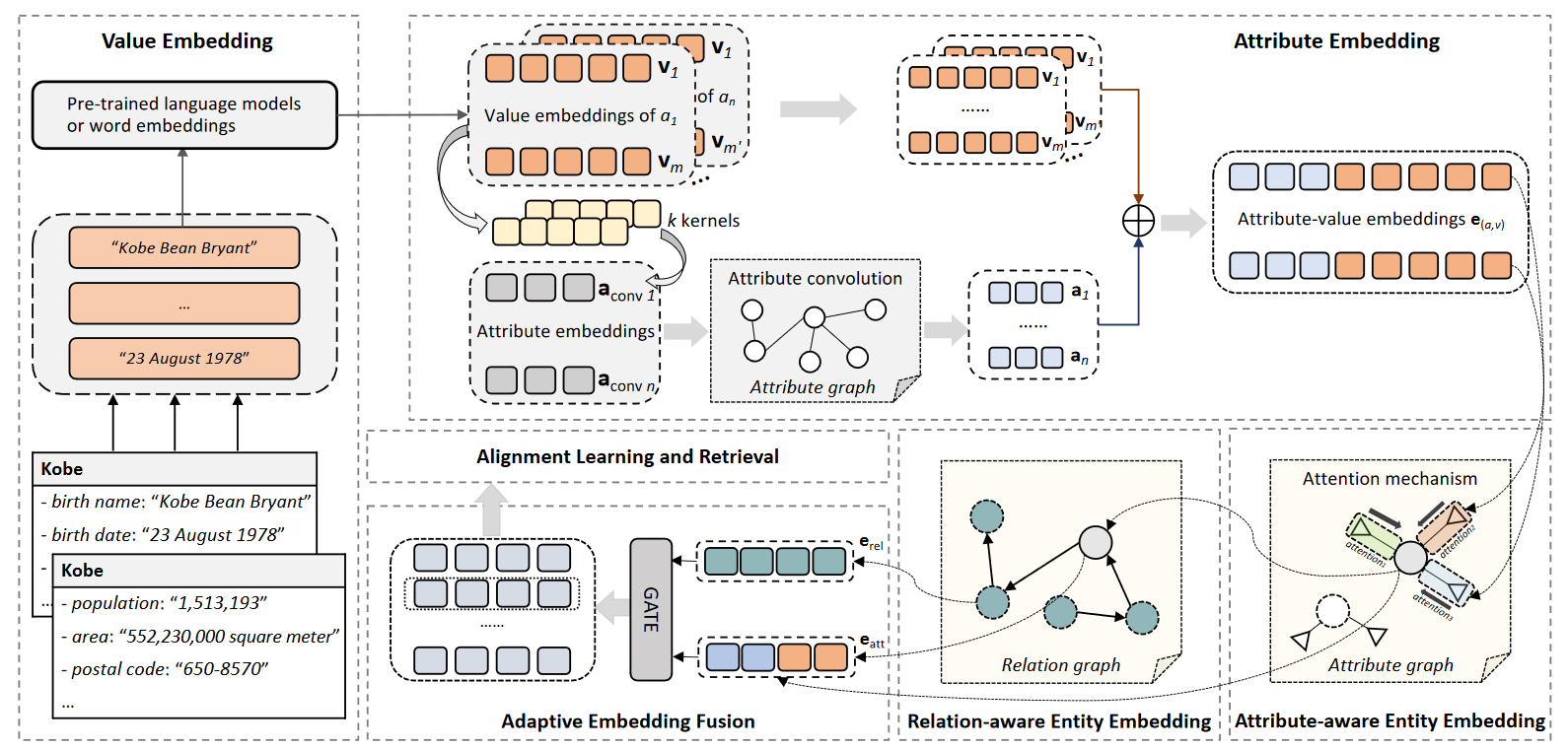
值嵌入:
对于字面值,首先使用预训练语言模型BERT或fastText嵌入,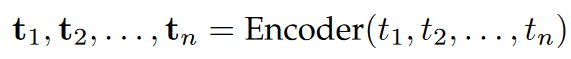
字面值可以表示为token嵌入的和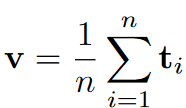
值嵌入用于属性嵌入,语言模型本身不参与训练
属性嵌入:
首先提取出属性a所有属性值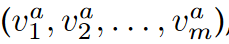
然后在嵌入上应用卷积层,利用平均池化合并这些表示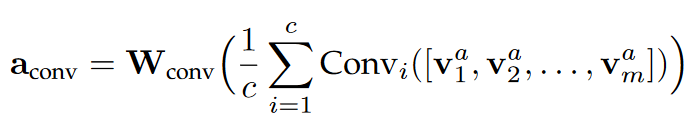
还要结合其它属性,需要创建一个属性图,节点是属性边是同时出现的频率
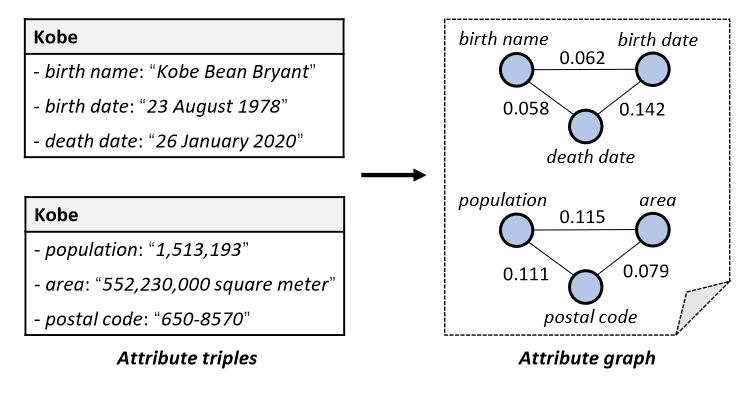
权重计算
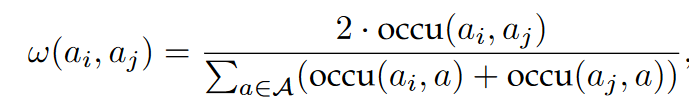
利用GCN学习属性嵌入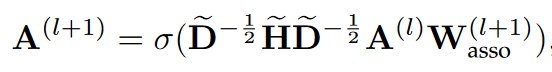
$\tilde\mathbf H$是属性关系邻接图
第一层输入是属性嵌入,利用sigmoid激活
属性感知的实体嵌入:
给定实体及其属性$(e,a,v)$
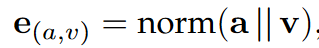
使用GAT学习端到端的实体嵌入,来发现重要实体
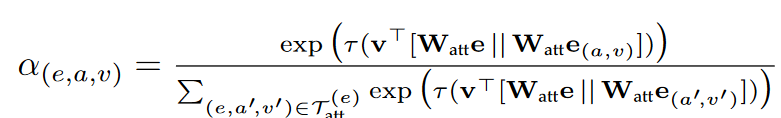
e的属性嵌入如下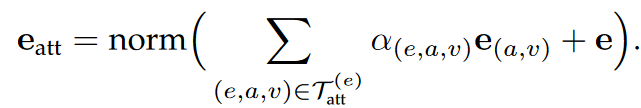
关系感知的实体嵌入:
如下等式计算实体e和关系r的权重
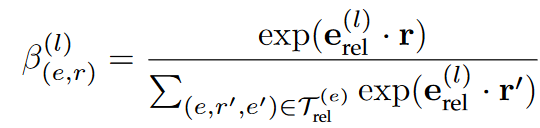
实体e如下表示
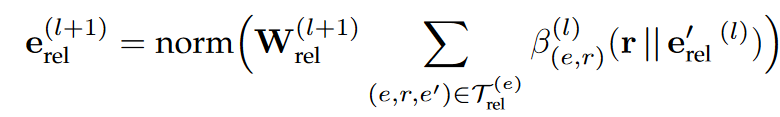
输入的获取为自适应嵌入融合:
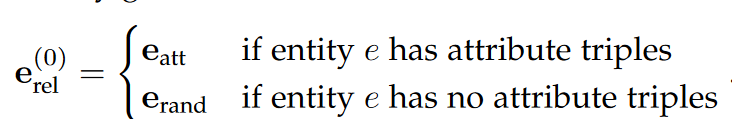
利用门控机制减少噪声传播
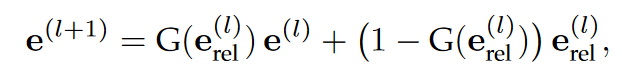
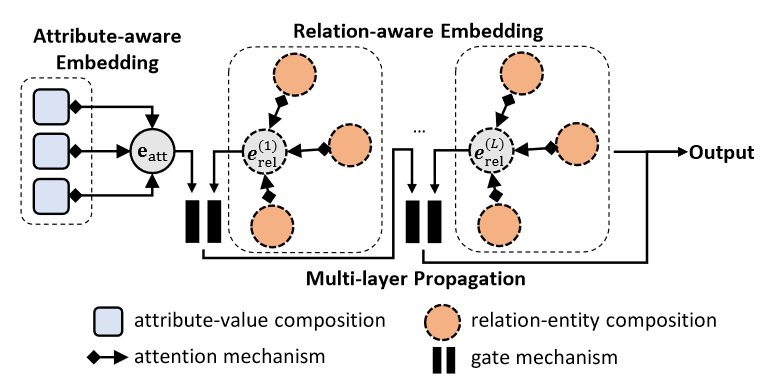
最终实体嵌入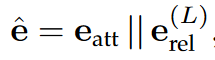
实体对齐:
多分类问题,但是每一个实体都有且只有一个标签。两个实体对齐的概率为:
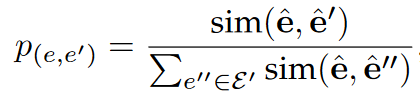
交叉熵损失函数计算对齐正确度

项目地址:https://github.com/nju-websoft/RoadEA
- 利用属性值和关系进行实体嵌入
- 门控机制控制属性值和关系的噪声传播
- 利用多分类机制实现实体对齐
Interactive Contrastive Learning for Self-Supervised Entity Alignment¶
交互对比学习
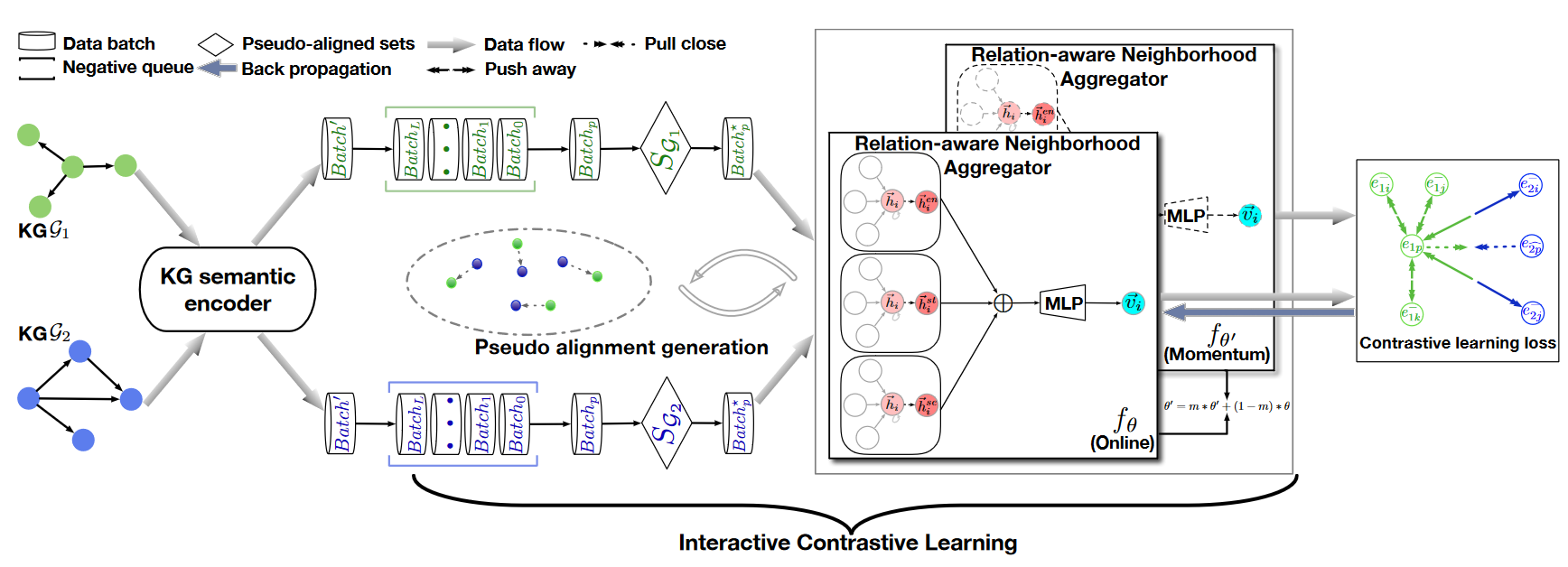
KG语义编码:LaBSE语言嵌入模型,利用SentenceTransformer获取实体描述嵌入
- KG名编码,
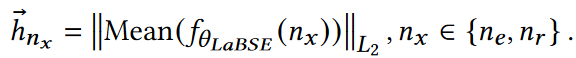
- 实体描述嵌入,选择前$L_{max}$个字符放入SentenceTransformers

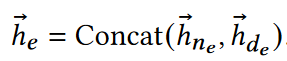
关系感知的邻居合并器:KG关系可以带来两部分信息:结构信息(邻居实体)和语义信息(邻居关系),利用GAT作为骨干网络
结构化合并器,vanilla GAT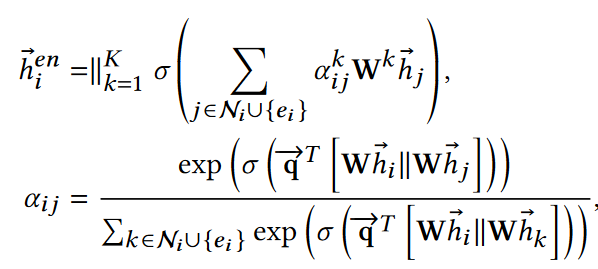
对邻接关系的重要性进行建模
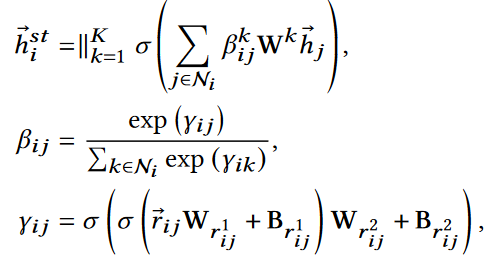
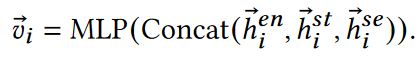
其中$h^{se}$是语义嵌入,基于邻居关系名获取
交互对比学习:
- 势能对比学习机制采用KG内部对比学习,让负样本之间距离比较远:给定一个初始嵌入$H_1$,目的是获取一个转换$V_1$,根据SelfKG,利用噪声对比估计(NCE)
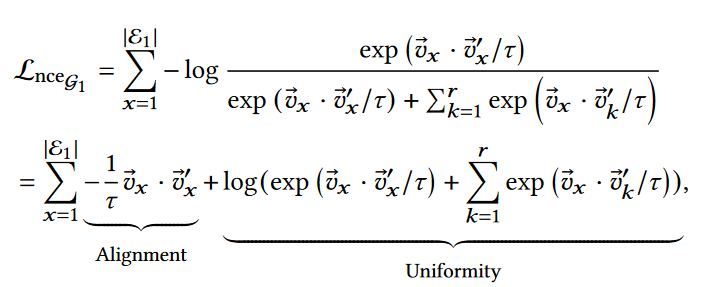
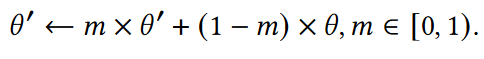
- 负采样队列将之前处理过的batch存储为正batch的负样本,可以提供大量的负样本。维护两个负样本队列,当新的数据batch到达时,添加到对应的负样本队列,同一个负样本队列的头$Batch_0$作为$Batch_p$出队。早期不采用任何参数更新,直到一个队列长度到达$L+1$,
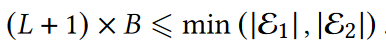
- 交互对比学习机制提供伪对齐对,作为信标,将正对样本和伪对齐样本靠近,并且远离负样本。

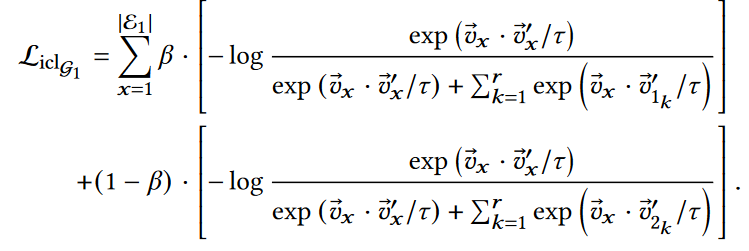
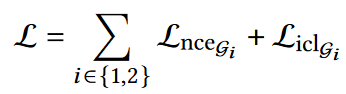
DivEA: "High-quality Task Division for Large-scale Entity Alignment"¶
Knowing the No-match: Entity Alignment with Dangling Cases¶
现实中两个待对齐的知识图谱往往有“Dangling Entities”,即在另一个知识图谱中没有对应实体,本文就是找出这样的实体并忽略掉
为了寻找Dangling实体,首先训练一个前馈NN进行实体分类,用于给实体打标签,1--Dangling实体,0--可匹配实体
给定x,输入特征表示是嵌入x和NN转换后的$x_{nn}$的不同,x是Dangling实体的置信度是$p(y=1|x)=sigmod(FNN(Mx-x_{nn}))$
假设D时Dangling实体集合,A是可匹配实体集合,对于$\forall x\in D\cup A$,计算交叉熵损失函数最小
$y_x$是实际标签,现实中Dangling实体和可匹配实体是非常不同的,会导致非常不同的分布
由于Dangling实体是噪音,所以在嵌入空间中单独表示,距离和可匹配实体更远,因此要在Dangling实体和采样NN之间添加一个margin,最小化损失函数
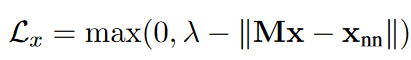
$\lambda$就是margin,这个损失函数和对齐损失函数组成了一个联合学习。没有对齐的实体之间的距离应该比对齐的实体之间的距离更大,Dangling实体在候选列表中应该有更低的优先级
背景排序:搜索实体的NN耗时、选择合适的margin也很难,基于经验研究,margin的选择很重要,基于开放集分类方法,让分类器对于未知类别的样本给同等惩罚,同样地:让孤立实体平等地远离任何目标空间实体,这让孤立实体成为了嵌入空间的“背景”,还减少了嵌入实体的规模,从而加大鼓励实体和可匹配实体的区别。
损失函数为
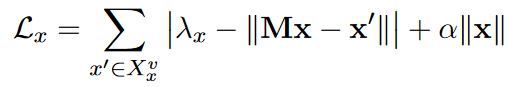
$\lambda_x$是平均距离,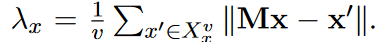 这样可以让相对靠近的实体远离,而不需要margin
这样可以让相对靠近的实体远离,而不需要margin
学习和推断:学习总体损失函数即结合对齐损失和孤立实体检测损失,推断也是结合对齐和孤立实体检测损失,NN方式依赖于前馈神经网络,margin排序方式依赖于预设的margin,
Dangling-Aware Entity Alignment with Mixed High-Order Proximities¶
全局高阶临近度: